The Compensation Principle II describes the compensation of unsufficient sharpness by increased SNR. The base for CPII was already shown in the forthies of last century by Mr. Rose. He did experiments on the visibility of small details in an image and showed that the visibility depends on sharpness and contrast to noise ratio. Ten years ago the Rose criterion was taken for the formula of visibility of small details:

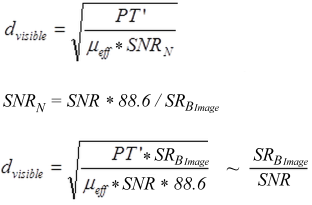
with dvisible as smallest visible detail, PT’ the perception threshold of an Individual, µeff as the effective attenuation coefficient depending on the energy and SNRN as SNR*88.6/SRB Image (and SRB Image as half of the inner unsharpness of the detector divided by the magnification).
In simple form the visibility of details depends on image sharpness and noise; higher unsharpness could be compensated with higher SNR.
This could be used if both IQI sensitivities (contrast sensitivity by wires or step holes and spatial resolution by duplex wire) cannot be achieved by the used detector system, an increase in single wire visibility or step hole visibility shall compensate too high unsharpness values. (i.e. if the required D12 and W14 is not achieved at the same time for a specific detector set-up, W15 and D11 provides an equivalent detection sensitivity).
The contrast sensitivity depends for digital detectors (DDA) on the used integration time and mA (tube current) for acquisition of the radiographic images for a given distance and tube voltage, so the single wire visibility or step hole visibility can be increased by increased exposure time and mA setting. This applies also for CR but with limitation by the max. achievable SNR due to the structure noise of the sensitive crystalline PSL layer.