In the upper post is a conflict:
increase the keV for a better SNR
and
reduce the keV for a better µ
eff.
What would be the optimum energy for an application?
Let us start with an example with an Aluminum stepwedge from 10 to 60mm - where the maximum power of the system is used (ISO-Watt: higher kV, lower mA - kV*mA=const.).
Hint: When the acceleration voltage is set to 120kV, the mean energy is 45keV only due to the distribution of energy by the tube.
For the three different acceleration voltages the system is set that in the free beam the signal is 100%.
At 10mm of AL with 90kV only 12.5% of the quants passes; at 120kV it is 30% and at 160kV 52.5%. The contrast at 90kV is much higher.
At 30mm of AL with 90kV only 0.2% of the quants passes - which is quite a dark image; at 120kV it is 2.7% and at 160kV 13.7%. The difference between 30mm and 31mm of AL would be hard to be detected when using 90kV.
At 60mm of AL nearly no quant passes with 90kV; with 120kV 0.075% and nearly 2% when using 160kV.
If 2% sensitivity is the requirement of your system you have to have in minimum 160kV if you have to inspect up to 60mm of AL.
The example with the signal or contrast of 1mm aditional Al on 30mm of AL is shown in the next graphs. The SNR will increase from 36 at 90kV to 250 at 160kV (+600%):
The specific contrast (signal difference from 30mm to 31mm) decreases from 5% with 90kV down to 3.8% with 160kV (-25%):
Finally the CNR of the 1mm material difference is important: It increases from 1.8 at 90kV up to 9.2 at 160kV:
Hint: In a lot of applications a minimum CNR of 2.5 is required.
It seems that higher energy is better always. But the two factors of reduced contrast and increased SNR will have an optimum (if you use a detector which is capable to do not saturate and resists the higher energies).
The amount of quants (intensity I) which passes the object of thickness w with the material constant µ in dependence of the energy E can be calculated by
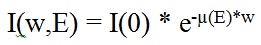
where I(0) is the energy on tube side of the object and I(w,E) behind the object.
The required energy for the best CNR can be calculated for an object with thickness T and a flaw of length w in direction of the beam by
The relative contrast C
rel is calculated for w small in respect to T as
and is nearly µ(E)*w.
With the noise [
sigma] in the X-ray image which has a Poisson distribution
sigma=
the CNR results to
The optimal contrast to noise ratio depends on the energy which itself depends on the absorption coefficient µ
The optimum is when one of the terms become Zero - which could only happen for the last term inside the (). If µ(E) = 2/T this term is Zero and the maximum CNR is at this energy.
With other words: The optimal energy level is where the absorption coefficient is half of the penetrated thickness. The values of µ for different energies and materials can be taken of the
.






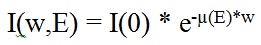 where I(0) is the energy on tube side of the object and I(w,E) behind the object.
where I(0) is the energy on tube side of the object and I(w,E) behind the object.